Overview

Here I will go incorporating charge separation (or electrification) interactions of specifically adsorbed anions within an electrochemical double layer (EDL). I will briefly go through some theory and the aGC-DFT approach, as well

1. Base Models of Acetate Adsorption: Low and High pH

Monovalent

Here, I review the basic derivations of anion adsorption without EDL considerations. More detailed derivations and basics are discussed in my previous blog posts.

High pH

When the pH is greater than the pKa of the acid of interest, anions are present due to the lack of proton concentration. Thus, the reaction to specifically adsorb anions on the metal is given as:

\[A^-_{(aq)}+ * \rightarrow A^*_{(aq)} + e^- (1)\]

The equilibrium adsorption potential is the electrode potential where this reaction is at equilibrium. Thus, the free energy of the reaction solved at the equilibrium adsorption potential is given as:

\[\Delta G_{ads}(U^0_{abs})=0=G_{A^*_{(g)}} -|e|U^0_{abs} - G_{A^-_{(g)}} - G_{*_{(g)}}+\Delta\Delta G_{solv} (2)\]

and the equilibrium adsorption potential for when the pH is above the pKa is given as:

\[U^0_{abs} = \frac{G_{A^*_{(g)}} - G_{A^-_{(g)}} - G_{*_{(g)}}+\Delta\Delta G_{solv}}{|e|} (3)\]

where this equilibrium potential can be converted to an experimentally relevant scale (ex: SHE).

Low pH

When the pH is below the pKa, there is a high proton concentration. Thus, “anions” are in the form as the undissociated acid (HA). The equation for the acid adsorb is given as:

\[HA_{(aq)}+ * \rightarrow A^*_{(aq)} + e^- + H^+ (4)\]

The Computational Hydrogen Electrode is used to approximate the free energy of the proton and electron pair, resulting in the free energy change to be:

\[\Delta G_{ads}(U_{RHE})=G_{A^*_{(g)}} + \frac{1}{2}G_{H_2,(g)} - |e|U_{RHE}- G_{HA_{(g)}} - G_{*} +\Delta\Delta G_{solv} (5)\]

which sets the potential on a RHE scale. The equilibrium potential can be solved analogously as shown in the high pH case. Alternatively, the RHE and SHE are related by the Nernstian change in the pH:

\[U_{RHE} = U_{SHE} - 0.059pH(6)\]

where Eq. 5 is written based on the SHE scale and the resulting form is given as Equation 7.

\[\Delta G_{ads}(U_{SHE})=G_{A^*_{(g)}} + \frac{1}{2}G_{H_2,(g)} - |e|U_{SHE} + 0.059pH- G_{HA_{(g)}} - G_{*} +\Delta\Delta G_{solv} (7)\]

The equilibrium adsorption potential can be solved similarly for when the reaction is at equilibrium, which nets the following:

\[U^0_{SHE} = \frac{G_{A^*_{(g)}} + \frac{1}{2}G_{H_2,(g)} + 0.059pH- G_{HA_{(g)}} - G_{*} +\Delta\Delta G_{solv}}{|e|} (8)\]

where the equilibrium adsorption potential is pH dependent based on a Nernstanian shift.

Non-monovalent Anions

Anions are certainly not only present as monovalent species. The following are brief derivations for the non-monovalent cases.

Divalent

Here I derive specific anion adsorption as for a divalent anion as a simple example.

When the pH > pKa, the divalent adsorbs onto the metal as:

\[A^{2-} + * \rightarrow A* + 2e^- (9)\]

When the pH < pKa, the diprotic adsorbs onto the metal as:

\[H_2A + * \rightarrow A^* +2(e^- + H^+) \;\;\;(10)\]

The procedure to solve for the equilibrium adsorption potential is the same as for the monovalent case.

General Form

Based on the divalent case, the adsorption of any polyvalent anion can be written in the following Equations 11 and 12.

\[A^{n-} + * \rightarrow A* + ne^- (11)\] \[H_nA + * \rightarrow A^* +n(e^- + H^+)\;\;\; (12)\]

where Equation 11 is applicable for when the pH > pKa and Equation 12 is applicable when the pH<pKa. The equilibrium adsorption potential for when the pH>pKa can then be calculated as:

\[\Delta G_{ads}(U^0_{abs})=0=G_{A^*_{(g)}} -n|e|U^0_{abs} - G_{A^-_{(g)}} - G_{*_{(g)}}+\Delta\Delta G_{solv} (13a)\] \[U^0_{abs} = \frac{G_{A^*_{(g)}} - G_{A^-_{(g)}} - G_{*_{(g)}}+\Delta\Delta G_{solv}}{n|e|} (13b)\]

When the pH<pKa, the equilibrium adsorption potential is calculated as:

\[\Delta G_{ads}(U_{RHE})=G_{A^*_{(g)}} + n(\frac{1}{2}G_{H_2,(g)} - |e|U_{RHE})- G_{HA_{(g)}} - G_{*} +\Delta\Delta G_{solv} (14a)\] \[\Delta G_{ads}(U_{SHE})=G_{A^*_{(g)}} + n(\frac{1}{2}G_{H_2,(g)} - |e|U_{SHE} + 0.059pH) - G_{HA_{(g)}} - G_{*} +\Delta\Delta G_{solv} (14 b)\] \[U^0_{SHE} = \frac{G_{A^*_{(g)}} + n(\frac{1}{2}G_{H_2,(g)} + 0.059pH)- G_{HA_{(g)}} - G_{*} +\Delta\Delta G_{solv}}{n|e|} (14c)\]

2. Implementing EDL effects using Analytical Grand Canonical DFT

Previously in Section 1, we did not incorporate the influence of electrification at the electrochemical double layer during the specific adsorption of an anion. Here in Section 2, we will discuss how to incorporate the influence of the EDL on 1) predicted equilibrium adsorption potential and 2) the electrosorption valency. We do this by incorporating these correction to constant potential and the electrification influence using our analytical Grand Canonical DFT framework (aGC-DFT).

While I briefly go over this model, detailed derivations and its applications of aGC-DFT should be done in our Journal of Catalysis paper and our Journal of Physical Chemistry paper of its applications for barriers. Additionally, a recent blog post I recently published further discusses the dilemma of correcting our simulations to “constant potential” to accurately model electrocatalysis.

2.1 Equilibrium Adsorption Potential

Analytical Grand Canonical DFT correction of Reaction States

The goal is to correct the free energy of either the adsorbed anion (A*) or the bare metal surface with EDL considerations. From the previous blog post, the Grand Canonical free energy of any reaction state, $\lambda$, with electrification considerations within the EDL and corrected to a potential is given as:

\[\Omega_{\lambda}(U) =G_{\lambda}(U) = G_{\lambda}(U_{pzc,\lambda})+E_{charging}+E_{field-ads}\; (15)\]

where $G_{\lambda}(U_{pzc,\lambda})$ is the free energy based on the “vacuum” DFT simulation of the reaction state $\lambda$, $E_{charging}$ is the energy to charge the potential of reaction state $\lambda$, to the potential of interest ($U$), and $E_{field-ads}$ is the field adsorbate interactions. From the previous blog post, we will assume a potential-independent capacitance to charge the reaction state to $U$ for simplicity, which yields:

\[E_{charging}=-\frac{1}{2}C(U-U_{pzc,\lambda})^2 \; (16)\]

where derivations for potential-dependent capacitance or charging energy is derived in the previous post. The field adsorbate interactions is given as a truncated second order Taylor’s expansion of the Energy w.r.t field as:

\[E(F)=E_{F=0}+\frac{dE}{dF}F+\frac{1}{2} \frac{d^2E}{dF^2}F^2+...\; (17a)\] \[E(F)=E_{F=0}+\mu_{(F=0)} F+\frac{1}{2} \alpha F^2+...\; (17b)\]

where $F$ is the Electric Field, $E_{F=0}$ is the DFT energy at $F$=0, $\mu_{(F=0)}$ is dipole moment of the reaction state when $F$=0, and $\alpha$ is the polarizability of the reaction state. The dipole moment and the $E_{F=0}$ are easily attained from a “stock” DFT simulation. Procedures for the polarizability requires a fitting procedure, which is explained in our prior work in the SI.. Essentially, the last two terms describes the energy contributions of the surface dipole interacting with an electric field and the induced surface dipole with an electric field.

Combining all of these contributions yield the fully corrected Grand Canonical Free Energy of a particular state as:

\[\Omega_{\lambda}(U) =G_{\lambda}(U) = G_{\lambda}(U_{pzc,\lambda})-\frac{1}{2}C(U-U_{pzc,\lambda})^2+\mu_{(F=0)} F+\frac{1}{2} \alpha F^2\; (18)\]

where the reaction state now considers 1) charging to the correct potential based on a potential-independent capacitance and 2) the field-adsorbate interactions to a second term.

EDL model of Choice and Calculating Equilibrium Adsorption Potentials

The final puzzle piece to utilizing Equation 18 is recognizing that the capacitance and the field requires a description of the EDL, which this is generally unknown. Here we assume a classical Helmholtz model due to its simplicity in approximating the capacitance and the field as:

\[C = \frac{\epsilon_r \epsilon_0 A}{d}\;(19)\] \[F=\frac{U-U_{pzc,\lambda}}{d}\;(20)\]

where the relative permittivity (dielectric constant) of the Helmholtz EDL is $\epsilon_r$, and the vacuum permittivity is $\epsilon_0$, A is the area of the DFT slab, and d is the Helmholtz EDL width. To learn more about the intricacies of the EDL and current models, my recent blog post covers this topic. Here, we know all the parameters except the dielectric constant of the EDL and the distance of the Helmholtz EDL. However, the powerful advantage of this approach is to be able to approximate the capacitance and field by guessing different values of the dielectric constant and EDL width.

Combining Eqs. 18, 19, and 20 yields the final equation to correcting the Reaction State Free energy based on a Helmholtz Model as:

\[\Omega_{\lambda}(U) = G_{\lambda}(U_{pzc,\lambda})-\frac{1}{2}\frac{\epsilon_r \epsilon_0 A}{d}(U-U_{pzc,\lambda})^2+\mu_{(F=0)} \frac{U-U_{pzc,\lambda}}{d}+\frac{1}{2} \alpha (\frac{U-U_{pzc,\lambda}}{d})^2\; (21)\]

This may look complicated but luckily a code is provided in the former sections to tabulate all of these values. Additionally, by guessing different values of $\epsilon_r$ and $d$, we can calculate the energy of the reaction state with the free energy change. This can be seen for calculating the equilibrium adsorption potential using the monovalent high pH case of Equation 2 as modified as:

\[\Delta G_{ads}(U)=\Omega_{A^*_{(g)}}(U) -|e|U - G_{A^-_{(g)}} - \Omega_{*_{(g)}}(U)+\Delta\Delta G_{solv} (22a)\] \[\Delta G_{ads}(U^0_{abs})=0=\Omega_{A^*_{(g)}}(U^0_{abs}) -|e|U^0_{abs} - G_{A^-_{(g)}} - \Omega_{*_{(g)}}(U^0_{abs})+\Delta\Delta G_{solv} (22b)\]

where note the $\Omega$. Now this procedure can be used to calculate the Equilibrium Adsorption potential with EDL considerations.

2.2 Electrosorption Valency

In section 1, anions are assumed to undergo complete electron transfer. This is seen as A* in Eqs. 1,4,9 and 11. This is true if anions adsorb at a metal surface in vacuum, where the anion is complete neutralized and under go integer electron transfer. This is not true when at a non-vacuum interface or specifically at the Electrochemical double layer. This non-integer electron transfer is seen in electrocatalysis experimentally. One can view this non-interge as once the ion adsorbs, it can partially share electrons with the metal (donate or receive) to charge the double layer or interact with the environment. This is seen from the electrosorption valency, a measure of the degree of partial electron transfer to the surface. More readings regarding the electrosorption valency and charge transfer can be read here.

The electrosorption valency is the measure of the degree of partial electron transfer to the surface which the formula and its units are given as:

\[l = \frac{d\Delta G_{ads}}{dU}[=]\frac{eV}{V}[=]{e}\; (23)\]

Using Equations 22a and 23 yields the following equation describing the electrosorption valency of specific anion adsorption:

\[l(U) = \frac{d\Delta G_{ads}}{dU}=-|e| + 2\frac{\Delta \mu}{d} - \frac{\Delta (\alpha \mu)}{\epsilon A d^2} + \frac{\Delta \alpha}{d^2}U \;(24)\]

where the electrosorption valency depends on the dipole moment and polarizability changes between the adsorbed anion state and the bare metal surface. If the anion had no dipole moment and polarizability change upon adsorption (the last three terms are neglect), the electrosorption valency is negative one, indicating the one whole electron is transferred from the surface to the ion and the anion is neutralized. If the anion has a significant dipole moment and/or polarizability change, the electrosorption valency deviates from negative one. Electrosorption valency values more negative than negative one indicates that the metal transfer more than 1 electron to the anion, thus the anion retains a negative charge. Note that the electrosorption valency becomes potential dependent when the last term is significant aka the polarizability change is significant.

3. Python Code

Luckily, I wrote a Python script that uses that analyzes the data above. The script can be found in the DFTAnionAdsorption GitHub repo. The excel sheet of data needed must be obtained by emailing me at ajwongphd@gmail.com. The code does the following:

Export Data from Excel Sheet using Pandas
By specifying the pH and pKa, Calculate Equilibrium adsorption potentials and Electrosorption Valencies for different EDL parameters.
Plot the Equilibrium adsorption potentials and electrosorption valencyies across descriptors of interests (here we consider the Work Function, O* binding, and OH* binding.)
Code Inputs

Here, I will go over the inputs required in the Python Script.

Data Inputs using Pandas:

First, pandas exports each column of the excel template provided (DFTanionadsorption/ExcelSheets/Acetate_O_OH_Metals_Template.xlsx) as a dataframe to work with the data. The path and the sheet in the excel sheet must be specified. This is shown below.

```python
#%% Inputs by extracting Excel data

# Input Sheet Name and Path below
sheet = '111' # 110 or 111
path = "C:/Users/Drew Wong/.../Acetate_O_OH_Metals.xlsx"

#Code: Imports Data
df = pd.read_excel(path, sheet_name=sheet)
```

The rest of the generating the inputs is self-explainatory. Note that the analytical GC-DFT framework does not incorporate explicit solvent considerations. This is easily incorporated as $\Delta\Delta G_{solv}$ based on whatever treatment of solvation you wish to use. In the code, we assume it to be zero as follows:

```
g_solv = 0 # Solvation energies are zero for now, can input a list or array
```

This will need to be changed to be as a list or array for each metal of interest.

pH and pKa:

Since anion adsorption is dependent on the pH and pKa, these values will need to be user-inputs. This is shown below:

```
# Values of pH
pH=0 #pH to calculate shift 
pKa = 3.76 #Reference pKa 
n = 1 #Valency

# Example Input for pH level
if pH  > pKa:
    pH_level = "high"  # "high" or "low" relative to the pKa of interest
else:
    pH_level = "low"  # "high" or "low" relative to the pKa of interest  

```

Based on the pH and pKa, it will calculate the equilibrium adsorption differently depending if the pH is greater or less than the pKa as discussed before.

Potential Range:

Both the equilibrium adsorption potential and especially the electrosorption valency depends on the potential range used. For the allter, this is especially important for the electrosorption valency as it is potential dependent with the full model consideration of the aGC-DFT framework. Here, we calculate an “effective” electrosorption valency over a potential range specified, which is just the average electrosorption valency. The potential range inputs are defined below.

```
#Potential Range of Interest
u_low = -1 #Lower Potential V-SHE that you input
u_high = 2 #Upper Potential V-SHE 
u = np.linspace(u_low,u_high,25)
```

EDL Parameters:

The specified EDL parameters are specified as a list shown below:

```
er = [1,2,8,13,78.4] #Relative permittivity (Dielectric Constant)
d = [3,4.5,6,10] #Helmholtz EDL Width in Angstrom
```

Any plausiable value can be used. Note that in the code analysis that the “circle” markers extracts a combination from the specified er and d as shown:

```
plot_values = [resultsEDL[(2, 3), element]['u0_2c'] for element in elements] #Plot the value of U0 at er = 2 and d=3, which you can change to whatever value
```

An error will show if the combination chosen isn’t specified previously as these are just stored as a dictionary.

Conversion from absolute scale to the SHE

This conversion needs to be specified as shown below:

```
vac_nhe = 4.6 #abs to SHE
```

4.6 is a common value but this can range from 4.2 to 5.2 V.

Outputs

The following examples are the output of this code. Note the marker is the equilibrium potential or electrosorption valency at a specific dielectric constant and EDL width. The error bars are the range of these values for different EDL parameters.

Equilibrium Adsorption Potentials Correlating with Metal Descriptors

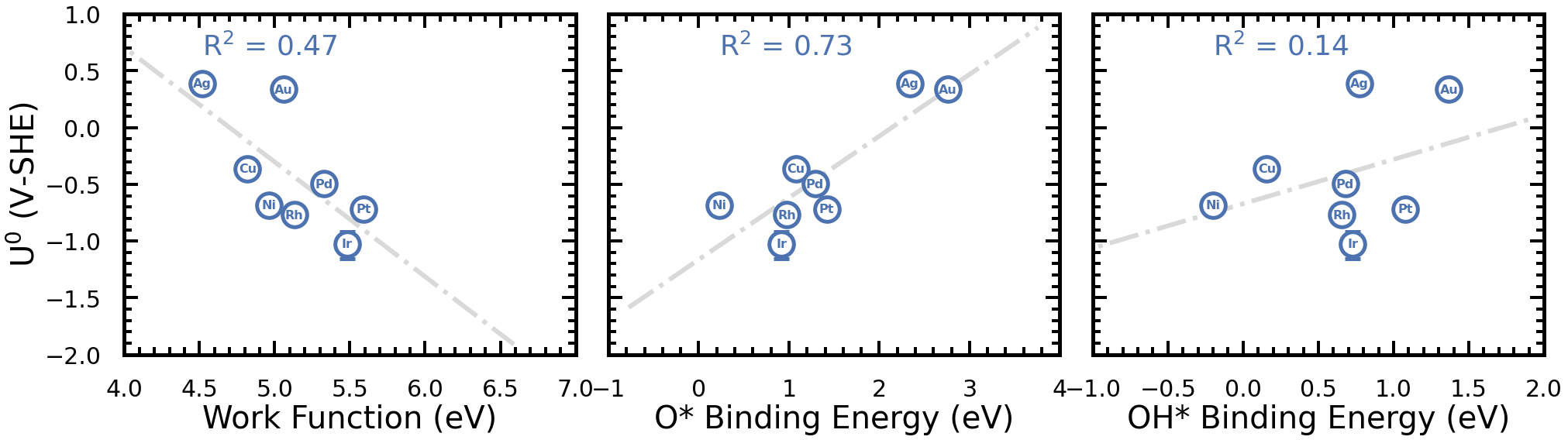
Here the equilibrium adsorption potential (of acetate adsorption) for different dielectric constants and EDL widths are plotted against various metal descriptors. This is shown for the case of (111) late-transition metal surfaces when the pH < pKa. The markers are the equilibrium adsorption potentials at a dielectric constant of 2 and a EDL width of 3 angstroms. Here, we observed that the O* binding may be a potential descriptor for acetate adsorption on (111) metal surfaces.

Electrosorption Valencies

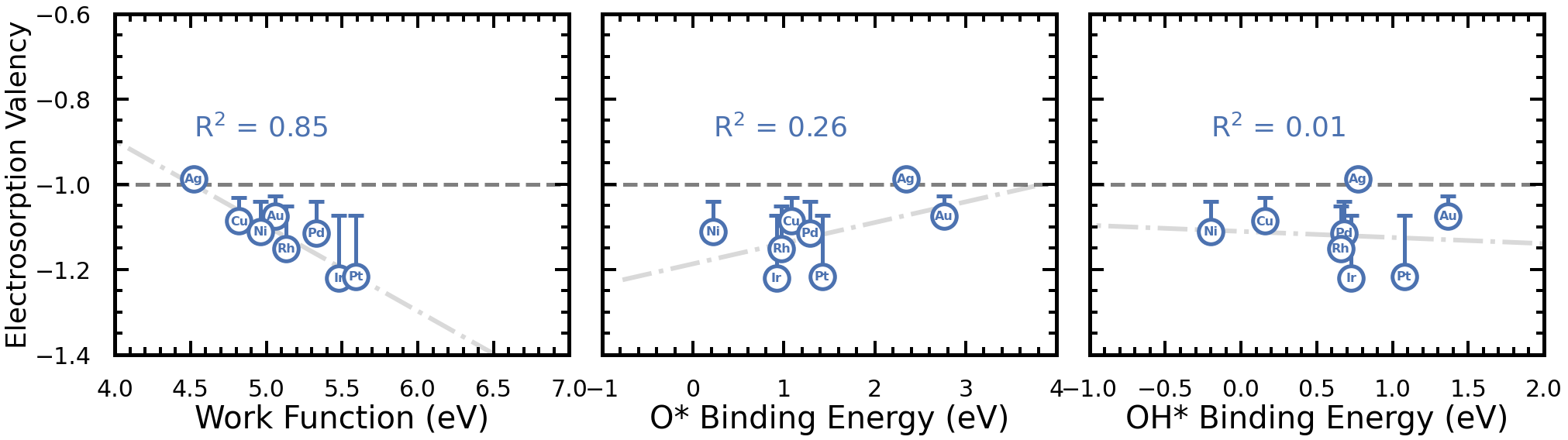
Similarly, the electrosorption valency of acetate adsorbed on different metals is plotted against the same metal descriptors. Note, that the electrosorption valency is usually more negative than -1. If the $l = -1$ like for Acetate on Ag(111), the adsorbed acetate undergoes approximately one electron transfer from the metal to the anion, neutralizing acetate to have a neutral charge. However, most metals $l < -1$, indicating that more than one (non-integer) electron is transfered to the anion like on Pt(111) with $l = -1.2$. This would indicate that surface-bound acetate exhibits a partial negative charge (i.e. -0.2 for Pt(111)). Interestingly, the work function of the metal may be indicative of the propensity of the anion to exhibit a more negative electrosorption valency.

4. References

If you enjoyed this post and want to learn more, I have provided additional reading and scripts that are related.

Scripts: Python scripts to replicate this work are placed in the DFTAnionAdsorption GitHub repo.

Readings: A review of anion adsorption and its pH dependence is discussed in my previous blog post. Electrosorption Valency and Partial Charge Transfer in Halides To learn more about the intricacies of the EDL and current models, my recent blog post covers this topic.